82. Competitive Equilibria with Arrow Securities#
82.1. Introduction#
This lecture presents Python code for experimenting with competitive equilibria of an infinite-horizon pure exchange economy with
Heterogeneous agents
Endowments of a single consumption that are person-specific functions of a common Markov state
Complete markets in one-period Arrow state-contingent securities
Discounted expected utility preferences of a kind often used in macroeconomics and finance
Common expected utility preferences across agents
Common beliefs among agents
A constant relative risk aversion (CRRA) one-period utility function that implies the existence of a representative consumer whose consumption process can be plugged into a formula for the pricing kernel for one-step Arrow securities and thereby determine equilibrium prices before determining an equilibrium distribution of wealth
Differences in their endowments make individuals want to reallocate consumption goods across time and Markov states
We impose restrictions that allow us to Bellmanize competitive equilibrium prices and quantities
We use Bellman equations to describe
asset prices
continuation wealth levels for each person
state-by-state natural debt limits for each person
In the course of presenting the model we shall encounter these important ideas
a resolvent operator widely used in this class of models
absence of borrowing limits in finite horizon economies
state-by-state borrowing limits required in infinite horizon economies
a counterpart of the law of iterated expectations known as a law of iterated values
a state-variable degeneracy that prevails within a competitive equilibrium and that opens the way to various appearances of resolvent operators
82.2. The setting#
In effect, this lecture implements a Python version of the model presented in section 9.3.3 of Ljungqvist and Sargent [Ljungqvist and Sargent, 2018].
82.2.1. Preferences and endowments#
In each period \(t\geq 0\), a stochastic event \(s_t \in {\bf S}\) is realized.
Let the history of events up until time \(t\) be denoted \(s^t = [s_0, s_{1}, \ldots, s_{t-1}, s_t]\).
(Sometimes we inadvertently reverse the recording order and denote a history as \(s^t = [s_t, s_{t-1}, \ldots, s_1, s_0]\).)
The unconditional probability of observing a particular sequence of events \(s^t\) is given by a probability measure \(\pi_t(s^t)\).
For \(t > \tau\), we write the probability of observing \(s^t\) conditional on the realization of \(s^\tau\)as \(\pi_t(s^t\vert s^\tau)\).
We assume that trading occurs after observing \(s_0\), which we capture by setting \(\pi_0(s_0)=1\) for the initially given value of \(s_0\).
In this lecture we shall follow much macroeconomics and econometrics and assume that \(\pi_t(s^t)\) is induced by a Markov process.
There are \(K\) consumers named \(k=1, \ldots , K\).
Consumer \(k\) owns a stochastic endowment of one good \(y_t^k(s^t)\) that depends on the history \(s^t\).
The history \(s^t\) is publicly observable.
Consumer \(k\) purchases a history-dependent consumption plan \(c^k = \{c_t^k(s^t)\}_{t=0}^\infty\)
Consumer \(k\) orders consumption plans by
where \(0 < \beta < 1\).
The right side is equal to \( E_0 \sum_{t=0}^\infty \beta^t u_k(c_t^k) \), where \(E_0\) is the mathematical expectation operator, conditioned on \(s_0\).
Here \(u_k(c)\) is an increasing, twice continuously differentiable, strictly concave function of consumption \(c\geq 0\) of one good.
The utility function of person \(k\) satisfies the Inada condition
This condition implies that each agent chooses strictly positive consumption for every date-history pair \((t, s^t)\).
Those interior solutions enable us to confine our analysis to Euler equations that hold with equality and also guarantee that natural debt limits don’t bind in economies like ours with sequential trading of Arrow securities.
We adopt the assumption, routinely employed in much of macroeconomics, that consumers share probabilities \(\pi_t(s^t)\) for all \(t\) and \(s^t\).
A feasible allocation satisfies
for all \(t\) and for all \(s^t\).
82.3. Recursive Formulation#
Following descriptions in section 9.3.3 of Ljungqvist and Sargent [Ljungqvist and Sargent, 2018] chapter 9, we set up a competitive equilibrium of a pure exchange economy with complete markets in one-period Arrow securities.
When endowments \(y^k(s)\) are all functions of a common Markov state \(s\), the pricing kernel takes the form \(Q(s'|s)\), where \(Q(s'| s)\) is the price of one unit of consumption in state \(s'\) at date \(t+1\) when the Markov state at date \(t\) is \(s\).
These enable us to provide a recursive formulation of a consumer’s optimization problem.
Consumer \(k\)’s state at time \(t\) is its financial wealth \(a^k_t\) and Markov state \(s_t\).
Let \(v^k(a,s)\) be the optimal value of consumer \(k\)’s problem starting from state \((a, s)\).
\(v^k(a,s)\) is the maximum expected discounted utility that consumer \(k\) with current financial wealth \(a\) can attain in Markov state \(s\).
The optimal value function satisfies the Bellman equation
where maximization is subject to the budget constraint
and also the constraints
with the second constraint evidently being a set of state-by-state debt limits.
Note that the value function and decision rule that solve the Bellman equation implicitly depend on the pricing kernel \(Q(\cdot \vert \cdot)\) because it appears in the agent’s budget constraint.
Use the first-order conditions for the problem on the right of the Bellman equation and a Benveniste-Scheinkman formula and rearrange to get
where it is understood that \(c_t^k = c^k(s_t)\) and \(c_{t+1}^k = c^k(s_{t+1})\).
A recursive competitive equilibrium is an initial distribution of wealth \(\vec a_0\), a set of borrowing limits \(\{\bar A^k(s)\}_{k=1}^K\), a pricing kernel \(Q(s' | s)\), sets of value functions \(\{v^k(a,s)\}_{k=1}^K\), and decision rules \(\{c^k(s), \hat a^k(s)\}_{k=1}^K\) such that
The state-by-state borrowing constraints satisfy the recursion
For all \(k\), given \(a^k_0\), \(\bar A^k(s)\), and the pricing kernel, the value functions and decision rules solve the consumers’ problems;
For all realizations of \(\{s_t\}_{t=0}^\infty\), the consumption and asset portfolios \(\{\{c^k_t,\) \(\{\hat a^k_{t+1}(s')\}_{s'}\}_k\}_t\) satisfy \(\sum_k c^k_t = \sum_k y^k(s_t)\) and \(\sum_k \hat a_{t+1}^k(s') = 0\) for all \(t\) and \(s'\).
The initial financial wealth vector \(\vec a_0\) satisfies \(\sum_{k=1}^K a_0^k = 0 \).
The third condition asserts that there are zero net aggregate claims in all Markov states.
The fourth condition asserts that the economy is closed and starts from a situation in which there are zero net aggregate claims.
82.4. State Variable Degeneracy#
Please see Ljungqvist and Sargent [Ljungqvist and Sargent, 2018] for a description of timing protocol for trades consistent with an Arrow-Debreu vision in which
at time \(0\) there are complete markets in a complete menu of history \(s^t\)-contingent claims on consumption at all dates that all trades occur at time zero
all trades occur once and for all at time \(0\)
If an allocation and pricing kernel \(Q\) in a recursive competitive equilibrium are to be consistent with the equilibrium allocation and price system that prevail in a corresponding complete markets economy with such history-contingent commodities and all trades occurring at time \(0\), we must impose that \(a_0^k = 0\) for \(k = 1, \ldots , K\).
That is what assures that at time \(0\) the present value of each agent’s consumption equals the present value of his endowment stream, the single budget constraint in arrangement with all trades occurring at time \(0\).
Starting the system with \(a_0^k =0\) for all \(i\) has a striking implication that we call state variable degeneracy.
Here is what we mean by state variable degeneracy:
Although two state variables \(a,s\) appear in the value function \(v^k(a,s)\), within a recursive competitive equilibrium starting from \(a_0^k = 0 \ \forall i\) at initial Markov state \(s_0\), two outcomes prevail:
\(a_0^k = 0 \) for all \(i\) whenever the Markov state \(s_t\) returns to \(s_0\).
Financial wealth \(a\) is an exact function of the Markov state \(s\).
The first finding asserts that each household recurrently visits the zero financial wealth state with which it began life.
The second finding asserts that within a competitive equilibrium the exogenous Markov state is all we require to track an individual.
Financial wealth turns out to be redundant because it is an exact function of the Markov state for each individual.
This outcome depends critically on there being complete markets in Arrow securities.
For example, it does not prevail in the incomplete markets setting of this lecture The Aiyagari Model
82.5. Markov Asset Prices#
Let’s start with a brief summary of formulas for computing asset prices in a Markov setting.
The setup assumes the following infrastructure
Markov states: \(s \in S = \left[\bar{s}_1, \ldots, \bar{s}_n \right]\) governed by an \(n\)-state Markov chain with transition probability
A collection \(h=1,\ldots, H\) of \(n \times 1\) vectors of \(H\) assets that pay off \(d^h\left(s\right)\) in state \(s\)
An \(n \times n\) matrix pricing kernel \(Q\) for one-period Arrow securities, where \( Q_{ij}\) = price at time \(t\) in state \(s_t = \bar s_i\) of one unit of consumption when \(s_{t+1} = \bar s_j\) at time \(t+1\):
The price of risk-free one-period bond in state \(i\) is \(R_i^{-1} = \sum_{j}Q_{i,j}\)
The gross rate of return on a one-period risk-free bond Markov state \(\bar s_i\) is \(R_i = (\sum_j Q_{i,j})^{-1}\)
82.5.1. Exogenous Pricing Kernel#
At this point, we’ll take the pricing kernel \(Q\) as exogenous, i.e., determined outside the model
Two examples would be
\( Q = \beta P \) where \(\beta \in (0,1) \)
\(Q = S P \) where \(S\) is an \(n \times n\) matrix of stochastic discount factors
We’ll write down implications of Markov asset pricing in a nutshell for two types of assets
the price in Markov state \(s\) at time \(t\) of a cum dividend stock that entitles the owner at the beginning of time \(t\) to the time \(t\) dividend and the option to sell the asset at time \(t+1\). The price evidently satisfies \(p^h(\bar s_i) = d^h(\bar s_i) + \sum_j Q_{ij} p^h(\bar s_j) \), which implies that the vector \(p^h\) satisfies \(p^h = d^h + Q p^h\) which implies the formula
the price in Markov state \(s\) at time \(t\) of an ex dividend stock that entitles the owner at the end of time \(t\) to the time \(t+1\) dividend and the option to sell the stock at time \(t+1\). The price is
Note
The matrix geometric sum \((I - Q)^{-1} = I + Q + Q^2 + \cdots \) is an example of a resolvent operator.
Below, we describe an equilibrium model with trading of one-period Arrow securities in which the pricing kernel is endogenous.
In constructing our model, we’ll repeatedly encounter formulas that remind us of our asset pricing formulas.
82.5.2. Multi-Step-Forward Transition Probabilities and Pricing Kernels#
The \((i,j)\) component of the \(\ell\)-step ahead transition probability \(P^\ell\) is
The \((i,j)\) component of the \(\ell\)-step ahead pricing kernel \(Q^\ell\) is
We’ll use these objects to state a useful property in asset pricing theory.
82.5.3. Laws of Iterated Expectations and Iterated Values#
A law of iterated values has a mathematical structure that parallels a law of iterated expectations
We can describe its structure readily in the Markov setting of this lecture
Recall the following recursion satisfied by \(j\) step ahead transition probabilites for our finite state Markov chain:
We can use this recursion to verify the law of iterated expectations applied to computing the conditional expectation of a random variable \(d(s_{t+j})\) conditioned on \(s_t\) via the following string of equalities
The pricing kernel for \(j\) step ahead Arrow securities satisfies the recursion
The time \(t\) value in Markov state \(s_t\) of a time \(t+j\) payout \(d(s_{t+j})\) is
The law of iterated values states
We verify it by pursuing the following a string of inequalities that are counterparts to those we used to verify the law of iterated expectations:
82.6. General Equilibrium#
Now we are ready to do some fun calculations.
We find it interesting to think in terms of analytical inputs into and outputs from our general equilibrium theorizing.
82.6.1. Inputs#
Markov states: \(s \in S = \left[\bar{s}_1, \ldots, \bar{s}_n \right]\) governed by an \(n\)-state Markov chain with transition probability
A collection of \(K \times 1\) vectors of individual \(k\) endowments: \(y^k\left(s\right), k=1,\ldots, K\)
An \(n \times 1\) vector of aggregate endowment: \(y\left(s\right) \equiv \sum_{k=1}^K y^k\left(s\right)\)
A collection of \(K \times 1\) vectors of individual \(k\) consumptions: \(c^k\left(s\right), k=1,\ldots, K\)
A collection of restrictions on feasible consumption allocations for \(s \in S\):
Preferences: a common utility functional across agents \( E_0 \sum_{t=0}^\infty \beta^t u(c^k_t) \) with CRRA one-period utility function \(u\left(c\right)\) and discount factor \(\beta \in (0,1)\)
The one-period utility function is
so that
82.6.2. Outputs#
An \(n \times n\) matrix pricing kernel \(Q\) for one-period Arrow securities, where \( Q_{ij}\) = price at time \(t\) in state \(s_t = \bar s_i\) of one unit of consumption when \(s_{t+1} = \bar s_j\) at time \(t+1\)
pure exchange so that \(c\left(s\right) = y\left(s\right)\)
a \(K \times 1\) vector distribution of wealth vector \(\alpha\), \(\alpha_k \geq 0, \sum_{k=1}^K \alpha_k =1\)
A collection of \(n \times 1\) vectors of individual \(k\) consumptions: \(c^k\left(s\right), k=1,\ldots, K\)
82.6.3. \(Q\) is the Pricing Kernel#
For any agent \(k \in \left[1, \ldots, K\right]\), at the equilibrium allocation, the one-period Arrow securities pricing kernel satisfies
where \(Q\) is an \(n \times n\) matrix
This follows from agent \(k\)’s first-order necessary conditions.
But with the CRRA preferences that we have assumed, individual consumptions vary proportionately with aggregate consumption and therefore with the aggregate endowment.
This is a consequence of our preference specification implying that Engle curves are affine in wealth and therefore satisfy conditions for Gorman aggregation
Thus,
for an arbitrary distribution of wealth in the form of an \(K \times 1\) vector \(\alpha\) that satisfies
This means that we can compute the pricing kernel from
Note that \(Q_{ij}\) is independent of vector \(\alpha\).
Key finding: We can compute competitive equilibrium prices prior to computing a distribution of wealth.
82.6.4. Values#
Having computed an equilibrium pricing kernel \(Q\), we can compute several values that are required to pose or represent the solution of an individual household’s optimum problem.
We denote an \(K \times 1\) vector of state-dependent values of agents’ endowments in Markov state \(s\) as
and an \(n \times 1\) vector of continuation endowment values for each individual \(k\) as
\(A^k\) of consumer \(k\) satisfies
where
In a competitive equilibrium of an infinite horizon economy with sequential trading of one-period Arrow securities, \(A^k(s)\) serves as a state-by-state vector of debt limits on the quantities of one-period Arrow securities paying off in state \(s\) at time \(t+1\) that individual \(k\) can issue at time \(t\).
These are often called natural debt limits.
Evidently, they equal the maximum amount that it is feasible for individual \(k\) to repay even if he consumes zero goods forevermore.
Remark: If we have an Inada condition at zero consumption or just impose that consumption be nonnegative, then in a finite horizon economy with sequential trading of one-period Arrow securities there is no need to impose natural debt limits. See the section on a Finite Horizon Economy below.
82.6.5. Continuation Wealth#
Continuation wealth plays an important role in Bellmanizing a competitive equilibrium with sequential trading of a complete set of one-period Arrow securities.
We denote an \(K \times 1\) vector of state-dependent continuation wealths in Markov state \(s\) as
and an \(n \times 1\) vector of continuation wealths for each individual \(k\) as
Continuation wealth \(\psi^k\) of consumer \(k\) satisfies
where
Note that \(\sum_{k=1}^K \psi^k = {0}_{n \times 1}\).
Remark: At the initial state \(s_0 \in \begin{bmatrix} \bar s_1, \ldots, \bar s_n \end{bmatrix}\), the continuation wealth \(\psi^k(s_0) = 0\) for all agents \(k = 1, \ldots, K\). This indicates that the economy begins with all agents being debt-free and financial-asset-free at time \(0\), state \(s_0\).
Remark: Note that all agents’ continuation wealths recurrently return to zero when the Markov state returns to whatever value \(s_0\) it had at time \(0\).
82.6.6. Optimal Portfolios#
A nifty feature of the model is that an optimal portfolio of a type \(k\) agent equals the continuation wealth that we just computed.
Thus, agent \(k\)’s state-by-state purchases of Arrow securities next period depend only on next period’s Markov state and equal
82.6.7. Equilibrium Wealth Distribution \(\alpha\)#
With the initial state being a particular state \(s_0 \in \left[\bar{s}_1, \ldots, \bar{s}_n\right]\), we must have
which means the equilibrium distribution of wealth satisfies
where \(V \equiv \left[I - Q\right]^{-1}\) and \(z\) is the row index corresponding to the initial state \(s_0\).
Since \(\sum_{k=1}^K V_z y^k = V_z y\), \(\sum_{k=1}^K \alpha_k = 1\).
In summary, here is the logical flow of an algorithm to compute a competitive equilibrium:
compute \(Q\) from the aggregate allocation and formula (82.1)
compute the distribution of wealth \(\alpha\) from the formula (82.4)
Using \(\alpha\) assign each consumer \(k\) the share \(\alpha_k\) of the aggregate endowment at each state
return to the \(\alpha\)-dependent formula (82.2) and compute continuation wealths
via formula (82.3) equate agent \(k\)’s portfolio to its continuation wealth state by state
We can also add formulas for optimal value functions in a competitive equilibrium with trades in a complete set of one-period state-contingent Arrow securities.
Call the optimal value functions \(J^k\) for consumer \(k\).
For the infinite horizon economy now under study, the formula is
where it is understood that \( u(\alpha_k y)\) is a vector.
82.7. Finite Horizon#
We now describe a finite-horizon version of the economy that operates for \(T+1\) periods \(t \in {\bf T} = \{ 0, 1, \ldots, T\}\).
Consequently, we’ll want \(T+1\) counterparts to objects described above, with one important exception: we won’t need borrowing limits.
borrowing limits aren’t required for a finite horizon economy in which a one-period utility function \(u(c)\) satisfies an Inada condition that sets the marginal utility of consumption at zero consumption to zero.
Nonnegativity of consumption choices at all \(t \in {\bf T}\) automatically limits borrowing.
82.7.1. Continuation Wealths#
We denote a \(K \times 1\) vector of state-dependent continuation wealths in Markov state \(s\) at time \(t\) as
and an \(n \times 1\) vector of continuation wealths for each individual \(k\) as
Continuation wealths \(\psi^k\) of consumer \(k\) satisfy
where
Note that \(\sum_{k=1}^K \psi_t^k = {0}_{n \times 1}\) for all \(t \in {\bf T}\).
Remark: At the initial state \(s_0 \in \begin{bmatrix} \bar s_1, \ldots, \bar s_n \end{bmatrix}\), for all agents \(k = 1, \ldots, K\), continuation wealth \(\psi_0^k(s_0) = 0\). This indicates that the economy begins with all agents being debt-free and financial-asset-free at time \(0\), state \(s_0\).
Remark: Note that all agents’ continuation wealths return to zero when the Markov state returns to whatever value \(s_0\) it had at time \(0\). This will recur if the Markov chain makes the initial state \(s_0\) recurrent.
With the initial state being a particular state \(s_0 \in \left[\bar{s}_1, \ldots, \bar{s}_n\right]\), we must have
which means the equilibrium distribution of wealth satisfies
where now in our finite-horizon economy
and \(z\) is the row index corresponding to the initial state \(s_0\).
Since \(\sum_{k=1}^K V_z y^k = V_z y\), \(\sum_{k=1}^K \alpha_k = 1\).
In summary, here is the logical flow of an algorithm to compute a competitive equilibrium with Arrow securities in our finite-horizon Markov economy:
compute \(Q\) from the aggregate allocation and formula (82.1)
compute the distribution of wealth \(\alpha\) from formulas (82.6) and (82.7)
using \(\alpha\), assign each consumer \(k\) the share \(\alpha_k\) of the aggregate endowment at each state
return to the \(\alpha\)-dependent formula (82.5) for continuation wealths and compute continuation wealths
equate agent \(k\)’s portfolio to its continuation wealth state by state
While for the infinite horizon economy, the formula for value functions is
for the finite horizon economy the formula is
where it is understood that \( u(\alpha_k y)\) is a vector.
82.8. Python Code#
We are ready to dive into some Python code.
As usual, we start with Python imports.
import numpy as np
import matplotlib.pyplot as plt
np.set_printoptions(suppress=True)
First, we create a Python class to compute the objects that comprise a competitive equilibrium with sequential trading of one-period Arrow securities.
In addition to infinite-horizon economies, the code is set up to handle finite-horizon economies indexed by horizon \(T\).
We’ll study examples of finite horizon economies after we first look at some infinite-horizon economies.
class RecurCompetitive:
"""
A class that represents a recursive competitive economy
with one-period Arrow securities.
"""
def __init__(self,
s, # state vector
P, # transition matrix
ys, # endowments ys = [y1, y2, .., yI]
γ=0.5, # risk aversion
β=0.98, # discount rate
T=None): # time horizon, none if infinite
# preference parameters
self.γ = γ
self.β = β
# variables dependent on state
self.s = s
self.P = P
self.ys = ys
self.y = np.sum(ys, 1)
# dimensions
self.n, self.K = ys.shape
# compute pricing kernel
self.Q = self.pricing_kernel()
# compute price of risk-free one-period bond
self.PRF = self.price_risk_free_bond()
# compute risk-free rate
self.R = self.risk_free_rate()
# V = [I - Q]^{-1} (infinite case)
if T is None:
self.T = None
self.V = np.empty((1, n, n))
self.V[0] = np.linalg.inv(np.eye(n) - self.Q)
# V = [I + Q + Q^2 + ... + Q^T] (finite case)
else:
self.T = T
self.V = np.empty((T+1, n, n))
self.V[0] = np.eye(n)
Qt = np.eye(n)
for t in range(1, T+1):
Qt = Qt.dot(self.Q)
self.V[t] = self.V[t-1] + Qt
# natural debt limit
self.A = self.V[-1] @ ys
def u(self, c):
"The CRRA utility"
return c ** (1 - self.γ) / (1 - self.γ)
def u_prime(self, c):
"The first derivative of CRRA utility"
return c ** (-self.γ)
def pricing_kernel(self):
"Compute the pricing kernel matrix Q"
c = self.y
n = self.n
Q = np.empty((n, n))
for i in range(n):
for j in range(n):
ratio = self.u_prime(c[j]) / self.u_prime(c[i])
Q[i, j] = self.β * ratio * P[i, j]
self.Q = Q
return Q
def wealth_distribution(self, s0_idx):
"Solve for wealth distribution α"
# set initial state
self.s0_idx = s0_idx
# simplify notations
n = self.n
Q = self.Q
y, ys = self.y, self.ys
# row of V corresponding to s0
Vs0 = self.V[-1, s0_idx, :]
α = Vs0 @ self.ys / (Vs0 @ self.y)
self.α = α
return α
def continuation_wealths(self):
"Given α, compute the continuation wealths ψ"
diff = np.empty((n, K))
for k in range(K):
diff[:, k] = self.α[k] * self.y - self.ys[:, k]
ψ = self.V @ diff
self.ψ = ψ
return ψ
def price_risk_free_bond(self):
"Give Q, compute price of one-period risk free bond"
PRF = np.sum(self.Q, axis=1)
self.PRF = PRF
return PRF
def risk_free_rate(self):
"Given Q, compute one-period gross risk-free interest rate R"
R = np.sum(self.Q, axis=1)
R = np.reciprocal(R)
self.R = R
return R
def value_functionss(self):
"Given α, compute the optimal value functions J in equilibrium"
n, T = self.n, self.T
β = self.β
P = self.P
# compute (I - βP)^(-1) in infinite case
if T is None:
P_seq = np.empty((1, n, n))
P_seq[0] = np.linalg.inv(np.eye(n) - β * P)
# and (I + βP + ... + β^T P^T) in finite case
else:
P_seq = np.empty((T+1, n, n))
P_seq[0] = np.eye(n)
Pt = np.eye(n)
for t in range(1, T+1):
Pt = Pt.dot(P)
P_seq[t] = P_seq[t-1] + Pt * β ** t
# compute the matrix [u(α_1 y), ..., u(α_K, y)]
flow = np.empty((n, K))
for k in range(K):
flow[:, k] = self.u(self.α[k] * self.y)
J = P_seq @ flow
self.J = J
return J
82.9. Examples#
We’ll use our code to construct equilibrium objects in several example economies.
Our first several examples will be infinite horizon economies.
Our final example will be a finite horizon economy.
82.9.1. Example 1#
Please read the preceding class for default parameter values and the following Python code for the fundamentals of the economy.
Here goes.
# dimensions
K, n = 2, 2
# states
s = np.array([0, 1])
# transition
P = np.array([[.5, .5], [.5, .5]])
# endowments
ys = np.empty((n, K))
ys[:, 0] = 1 - s # y1
ys[:, 1] = s # y2
ex1 = RecurCompetitive(s, P, ys)
# endowments
ex1.ys
array([[1., 0.],
[0., 1.]])
# pricing kernal
ex1.Q
array([[0.49, 0.49],
[0.49, 0.49]])
# Risk free rate R
ex1.R
array([1.02040816, 1.02040816])
# natural debt limit, A = [A1, A2, ..., AI]
ex1.A
array([[25.5, 24.5],
[24.5, 25.5]])
# when the initial state is state 1
print(f'α = {ex1.wealth_distribution(s0_idx=0)}')
print(f'ψ = \n{ex1.continuation_wealths()}')
print(f'J = \n{ex1.value_functionss()}')
α = [0.51 0.49]
ψ =
[[[-0. 0.]
[ 1. -1.]]]
J =
[[[71.41428429 70. ]
[71.41428429 70. ]]]
# when the initial state is state 2
print(f'α = {ex1.wealth_distribution(s0_idx=1)}')
print(f'ψ = \n{ex1.continuation_wealths()}')
print(f'J = \n{ex1.value_functionss()}')
α = [0.49 0.51]
ψ =
[[[-1. 1.]
[ 0. -0.]]]
J =
[[[70. 71.41428429]
[70. 71.41428429]]]
82.9.2. Example 2#
# dimensions
K, n = 2, 2
# states
s = np.array([1, 2])
# transition
P = np.array([[.5, .5], [.5, .5]])
# endowments
ys = np.empty((n, K))
ys[:, 0] = 1.5 # y1
ys[:, 1] = s # y2
ex2 = RecurCompetitive(s, P, ys)
# endowments
print("ys = \n", ex2.ys)
# pricing kernal
print ("Q = \n", ex2.Q)
# Risk free rate R
print("R = ", ex2.R)
ys =
[[1.5 1. ]
[1.5 2. ]]
Q =
[[0.49 0.41412558]
[0.57977582 0.49 ]]
R = [1.10604104 0.93477529]
# pricing kernal
ex2.Q
array([[0.49 , 0.41412558],
[0.57977582, 0.49 ]])
Note that the pricing kernal in example economies 1 and 2 differ.
This comes from differences in the aggregate endowments in state 1 and 2 in example 1.
ex2.β * ex2.u_prime(3.5) / ex2.u_prime(2.5) * ex2.P[0,1]
np.float64(0.4141255848169731)
ex2.β * ex2.u_prime(2.5) / ex2.u_prime(3.5) * ex2.P[1,0]
np.float64(0.5797758187437624)
# Risk free rate R
ex2.R
array([1.10604104, 0.93477529])
# natural debt limit, A = [A1, A2, ..., AI]
ex2.A
array([[69.30941886, 66.91255848],
[81.73318641, 79.98879094]])
# when the initial state is state 1
print(f'α = {ex2.wealth_distribution(s0_idx=0)}')
print(f'ψ = \n{ex2.continuation_wealths()}')
print(f'J = \n{ex2.value_functionss()}')
α = [0.50879763 0.49120237]
ψ =
[[[ 0. 0. ]
[ 0.55057195 -0.55057195]]]
J =
[[[122.907875 120.76397493]
[123.32114686 121.17003803]]]
# when the initial state is state 1
print(f'α = {ex2.wealth_distribution(s0_idx=1)}')
print(f'ψ = \n{ex2.continuation_wealths()}')
print(f'J = \n{ex2.value_functionss()}')
α = [0.50539319 0.49460681]
ψ =
[[[-0.46375886 0.46375886]
[-0. -0. ]]]
J =
[[[122.49598809 121.18174895]
[122.907875 121.58921679]]]
82.9.3. Example 3#
# dimensions
K, n = 2, 2
# states
s = np.array([1, 2])
# transition
λ = 0.9
P = np.array([[1-λ, λ], [0, 1]])
# endowments
ys = np.empty((n, K))
ys[:, 0] = [1, 0] # y1
ys[:, 1] = [0, 1] # y2
ex3 = RecurCompetitive(s, P, ys)
# endowments
print("ys = ", ex3.ys)
# pricing kernel
print ("Q = ", ex3.Q)
# Risk free rate R
print("R = ", ex3.R)
ys = [[1. 0.]
[0. 1.]]
Q = [[0.098 0.882]
[0. 0.98 ]]
R = [1.02040816 1.02040816]
# pricing kernel
ex3.Q
array([[0.098, 0.882],
[0. , 0.98 ]])
# natural debt limit, A = [A1, A2, ..., AI]
ex3.A
array([[ 1.10864745, 48.89135255],
[ 0. , 50. ]])
Note that the natural debt limit for agent \(1\) in state \(2\) is \(0\).
# when the initial state is state 1
print(f'α = {ex3.wealth_distribution(s0_idx=0)}')
print(f'ψ = \n{ex3.continuation_wealths()}')
print(f'J = \n{ex3.value_functionss()}')
α = [0.02217295 0.97782705]
ψ =
[[[ 0. -0. ]
[ 1.10864745 -1.10864745]]]
J =
[[[14.89058394 98.88513796]
[14.89058394 98.88513796]]]
# when the initial state is state 1
print(f'α = {ex3.wealth_distribution(s0_idx=1)}')
print(f'ψ = \n{ex3.continuation_wealths()}')
print(f'J = \n{ex3.value_functionss()}')
α = [0. 1.]
ψ =
[[[-1.10864745 1.10864745]
[ 0. 0. ]]]
J =
[[[ 0. 100.]
[ 0. 100.]]]
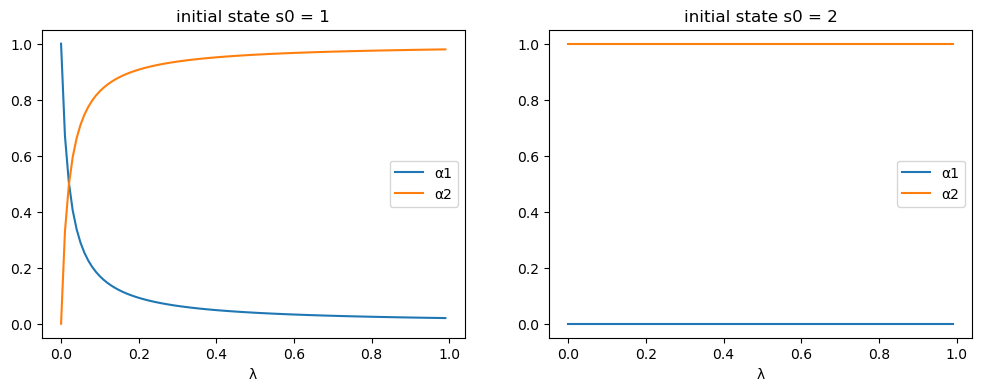
For the specification of the Markov chain in example 3, let’s take a look at how the equilibrium allocation changes as a function of transition probability \(\lambda\).
λ_seq = np.linspace(0, 0.99, 100)
# prepare containers
αs0_seq = np.empty((len(λ_seq), 2))
αs1_seq = np.empty((len(λ_seq), 2))
for i, λ in enumerate(λ_seq):
P = np.array([[1-λ, λ], [0, 1]])
ex3 = RecurCompetitive(s, P, ys)
# initial state s0 = 1
α = ex3.wealth_distribution(s0_idx=0)
αs0_seq[i, :] = α
# initial state s0 = 2
α = ex3.wealth_distribution(s0_idx=1)
αs1_seq[i, :] = α
fig, axs = plt.subplots(1, 2, figsize=(12, 4))
for i, αs_seq in enumerate([αs0_seq, αs1_seq]):
for j in range(2):
axs[i].plot(λ_seq, αs_seq[:, j], label=f'α{j+1}')
axs[i].set_xlabel('λ')
axs[i].set_title(f'initial state s0 = {s[i]}')
axs[i].legend()
plt.show()
82.9.4. Example 4#
# dimensions
K, n = 2, 3
# states
s = np.array([1, 2, 3])
# transition
λ = .9
μ = .9
δ = .05
# prosperous, moderate, and recession states
P = np.array([[1-λ, λ, 0], [μ/2, μ, μ/2], [(1-δ)/2, (1-δ)/2, δ]])
# endowments
ys = np.empty((n, K))
ys[:, 0] = [.25, .75, .2] # y1
ys[:, 1] = [1.25, .25, .2] # y2
ex4 = RecurCompetitive(s, P, ys)
# endowments
print("ys = \n", ex4.ys)
# pricing kernal
print ("Q = \n", ex4.Q)
# Risk free rate R
print("R = ", ex4.R)
# natural debt limit, A = [A1, A2, ..., AI]
print("A = \n", ex4.A)
print('')
for i in range(1, 4):
# when the initial state is state i
print(f"when the initial state is state {i}")
print(f'α = {ex4.wealth_distribution(s0_idx=i-1)}')
print(f'ψ = \n{ex4.continuation_wealths()}')
print(f'J = \n{ex4.value_functionss()}\n')
ys =
[[0.25 1.25]
[0.75 0.25]
[0.2 0.2 ]]
Q =
[[0.098 1.08022498 0. ]
[0.36007499 0.882 0.69728222]
[0.24038317 0.29440805 0.049 ]]
R = [0.84873434 0.51563476 1.71294115]
A =
[[-1.4141307 -0.45854174]
[-1.4122483 -1.54005386]
[-0.58434331 -0.3823659 ]]
when the initial state is state 1
α = [0.75514045 0.24485955]
ψ =
[[[ 0. 0. ]
[-0.81715447 0.81715447]
[-0.14565791 0.14565791]]]
J =
[[[-2.65741909 -1.51322919]
[-5.13103133 -2.92179221]
[-2.65649938 -1.51270548]]]
when the initial state is state 2
α = [0.47835493 0.52164507]
ψ =
[[[ 0.5183286 -0.5183286 ]
[ 0. -0. ]
[ 0.12191319 -0.12191319]]]
J =
[[[-2.11505328 -2.20868477]
[-4.08381377 -4.26460049]
[-2.11432128 -2.20792037]]]
when the initial state is state 3
α = [0.60446648 0.39553352]
ψ =
[[[ 0.28216299 -0.28216299]
[-0.37231938 0.37231938]
[ 0. -0. ]]]
J =
[[[-2.37756442 -1.92325926]
[-4.59067883 -3.71349163]
[-2.37674158 -1.92259365]]]
82.9.5. Finite Horizon Example#
We now revisit the economy defined in example 1, but set the time horizon to be \(T=10\).
# dimensions
K, n = 2, 2
# states
s = np.array([0, 1])
# transition
P = np.array([[.5, .5], [.5, .5]])
# endowments
ys = np.empty((n, K))
ys[:, 0] = 1 - s # y1
ys[:, 1] = s # y2
ex1_finite = RecurCompetitive(s, P, ys, T=10)
# (I + Q + Q^2 + ... + Q^T)
ex1_finite.V[-1]
array([[5.48171623, 4.48171623],
[4.48171623, 5.48171623]])
# endowments
ex1_finite.ys
array([[1., 0.],
[0., 1.]])
# pricing kernal
ex1_finite.Q
array([[0.49, 0.49],
[0.49, 0.49]])
# Risk free rate R
ex1_finite.R
array([1.02040816, 1.02040816])
In the finite time horizon case, ψ and J are returned as sequences.
Components are ordered from \(t=T\) to \(t=0\).
# when the initial state is state 2
print(f'α = {ex1_finite.wealth_distribution(s0_idx=0)}')
print(f'ψ = \n{ex1_finite.continuation_wealths()}\n')
print(f'J = \n{ex1_finite.value_functionss()}')
α = [0.55018351 0.44981649]
ψ =
[[[-0.44981649 0.44981649]
[ 0.55018351 -0.55018351]]
[[-0.40063665 0.40063665]
[ 0.59936335 -0.59936335]]
[[-0.35244041 0.35244041]
[ 0.64755959 -0.64755959]]
[[-0.30520809 0.30520809]
[ 0.69479191 -0.69479191]]
[[-0.25892042 0.25892042]
[ 0.74107958 -0.74107958]]
[[-0.21355851 0.21355851]
[ 0.78644149 -0.78644149]]
[[-0.16910383 0.16910383]
[ 0.83089617 -0.83089617]]
[[-0.12553824 0.12553824]
[ 0.87446176 -0.87446176]]
[[-0.08284397 0.08284397]
[ 0.91715603 -0.91715603]]
[[-0.04100358 0.04100358]
[ 0.95899642 -0.95899642]]
[[-0. -0. ]
[ 1. -1. ]]]
J =
[[[ 1.48348712 1.3413672 ]
[ 1.48348712 1.3413672 ]]
[[ 2.9373045 2.65590706]
[ 2.9373045 2.65590706]]
[[ 4.36204553 3.94415611]
[ 4.36204553 3.94415611]]
[[ 5.75829174 5.20664019]
[ 5.75829174 5.20664019]]
[[ 7.12661302 6.44387459]
[ 7.12661302 6.44387459]]
[[ 8.46756788 7.6563643 ]
[ 8.46756788 7.6563643 ]]
[[ 9.78170364 8.84460421]
[ 9.78170364 8.84460421]]
[[11.06955669 10.00907933]
[11.06955669 10.00907933]]
[[12.33165268 11.15026494]
[12.33165268 11.15026494]]
[[13.56850674 12.26862684]
[13.56850674 12.26862684]]
[[14.78062373 13.3646215 ]
[14.78062373 13.3646215 ]]]
# when the initial state is state 2
print(f'α = {ex1_finite.wealth_distribution(s0_idx=1)}')
print(f'ψ = \n{ex1_finite.continuation_wealths()}\n')
print(f'J = \n{ex1_finite.value_functionss()}')
α = [0.44981649 0.55018351]
ψ =
[[[-0.55018351 0.55018351]
[ 0.44981649 -0.44981649]]
[[-0.59936335 0.59936335]
[ 0.40063665 -0.40063665]]
[[-0.64755959 0.64755959]
[ 0.35244041 -0.35244041]]
[[-0.69479191 0.69479191]
[ 0.30520809 -0.30520809]]
[[-0.74107958 0.74107958]
[ 0.25892042 -0.25892042]]
[[-0.78644149 0.78644149]
[ 0.21355851 -0.21355851]]
[[-0.83089617 0.83089617]
[ 0.16910383 -0.16910383]]
[[-0.87446176 0.87446176]
[ 0.12553824 -0.12553824]]
[[-0.91715603 0.91715603]
[ 0.08284397 -0.08284397]]
[[-0.95899642 0.95899642]
[ 0.04100358 -0.04100358]]
[[-1. 1. ]
[-0. -0. ]]]
J =
[[[ 1.3413672 1.48348712]
[ 1.3413672 1.48348712]]
[[ 2.65590706 2.9373045 ]
[ 2.65590706 2.9373045 ]]
[[ 3.94415611 4.36204553]
[ 3.94415611 4.36204553]]
[[ 5.20664019 5.75829174]
[ 5.20664019 5.75829174]]
[[ 6.44387459 7.12661302]
[ 6.44387459 7.12661302]]
[[ 7.6563643 8.46756788]
[ 7.6563643 8.46756788]]
[[ 8.84460421 9.78170364]
[ 8.84460421 9.78170364]]
[[10.00907933 11.06955669]
[10.00907933 11.06955669]]
[[11.15026494 12.33165268]
[11.15026494 12.33165268]]
[[12.26862684 13.56850674]
[12.26862684 13.56850674]]
[[13.3646215 14.78062373]
[13.3646215 14.78062373]]]
We can check the results with finite horizon converges to the ones with infinite horizon as \(T \rightarrow \infty\).
ex1_large = RecurCompetitive(s, P, ys, T=10000)
ex1_large.wealth_distribution(s0_idx=1)
array([0.49, 0.51])
ex1.V, ex1_large.V[-1]
(array([[[25.5, 24.5],
[24.5, 25.5]]]),
array([[25.5, 24.5],
[24.5, 25.5]]))
ex1_large.continuation_wealths()
ex1.ψ, ex1_large.ψ[-1]
(array([[[-1., 1.],
[ 0., -0.]]]),
array([[-1., 1.],
[ 0., -0.]]))
ex1_large.value_functionss()
ex1.J, ex1_large.J[-1]
(array([[[70. , 71.41428429],
[70. , 71.41428429]]]),
array([[70. , 71.41428429],
[70. , 71.41428429]]))